The Quantum Threat to Cryptography

Written by:

Tunga Bayrak and SAM KIM

MARCH 22ND, 2024 | 17 minute read

Quantum Computing?

Quantum computing exploits superposition and entanglement to address problems beyond the reach of classical computers. At the same time, blockchain uses cryptographic techniques for secure, decentralized transaction recording. Understanding the intersection of these technologies reveals important shifts in cryptographic paradigms.

Unlike traditional computers that use binary bits (0s and 1s), quantum computers operate with qubits, capable of being in states 0, 1, or both simultaneously. This gives quantum computers exponential computing power and allows them to solve complex problems that would be practically impossible for any other computer.

The concept first emerged in the 1980s when Richard Feynman proposed using quantum computers for calculations and simulating quantum systems. Following that, in 1994, Shor developed a Quantum for Factorization Algorithm which made prime factorization of integers exponentially faster. This algorithm threatened the whole of RSA encryption which the Web depended on for security. More recently in 2019 Google achieved quantum supremacy using a 53-qubit processor that made a calculation that would take the best classical computer 10 thousand years to solve.

Current Developments in Quantum Computing

Just last December, IBM announced their first ever 1000+ qubit chip “Condor”, a remarkable achievement in qubit counts considering the 127 qubits they had just achieved in 2021. The increased qubit count helps with error correction and takes us one step closer to practical scalability.

For 30 years Shor’s Algorithm for Prime Factorization was the most efficient Quantum Algorithm for Factorization and there has been little to no improvements over it. However, very recently, Oded Regev, a computer scientist from New York University, made a groundbreaking improvement to Shor’s algorithm using high-dimensional geometry techniques from cryptography. His work has fundamentally increased the efficiency of the algorithm, optimizing the relationship between the size of the number being factored and the quantum operations required.

In a significant move, IBM unveiled its Heron processor near the end of 2023. Despite its seemingly modest 133 qubits, the Heron processor is designed for interconnectivity with other processors. This represents a paradigm shift towards modular quantum computing, where multiple processors can be linked together, enhancing scalability and computational power.

Beyond these groundbreaking achievements, numerous other companies are currently making advancements in Quantum Computing, with some specializing in hardware and others focusing on software solutions. 

This is all to say, quantum computing is real and we are getting ever closer to its practical scalability and it becoming a world-changing reality. 

Quantum Computing Defined

Several core metrics provide valuable insights into each company’s technical capabilities. Let’s use a car analogy to solidify the concepts:

Qubit Number: The count of qubits  in  a  Quantum  Processing  Unit  (QPU)  serves  as  an  indicator of its raw processing capabilities. A greater number of qubits generally suggests that a quantum computer possesses enhanced computational power, capable of managing intricate algorithms.

Analogous to: the horsepower of an automotive engine, representing raw power. Just as more horsepower in a car suggests it can achieve higher speeds and carry heavier loads, a higher number of qubits suggests a quantum computer can handle more complex algorithms and calculations.

Qubits   ←→  Raw Power/ Horsepower

Xanadu, Rigetti, and Intel have ambitious plans of scaling up to 1,000 to 4,000-qubit systems between 2024 to 2026, aligning with Microsoft’s vision of achieving a quantum machine with at least 1 million stable qubits (timeline not specified). In contrast, Google, IBM, and Amazon are already operational with qubits ranging from 70 to 433. D-Wave stands out with its 2000Q QPU boasting over 2000 qubits and the Advantage QPU exceeding 5000 qubits, showcasing a substantial quantum infrastructure. However, it's important to note, as with cars where horsepower isn't the only measure of performance, the sheer number of qubits doesn't directly translate to a superior quantum computer due to other factors like error rates and qubit quality.

Circuit Layer Operations Per Second (CLOPS): This metric was first proposed by IBM to measure how fast a quantum processor can execute circuits. A higher CLOPS indicates a system’s ability to perform more work in a given timeframe.

Analogous to: the transmission system of a car. The gears decide how efficiently the car uses its horsepower (qubit numbers) to actually move. CLOPS measures how efficiently a quantum computer uses its qubits to perform calculations. Just as a car with a more effective transmission system can better translate its horsepower into speed under various conditions, a higher CLOPS value indicates a quantum processor can execute more operations per second, enhancing its performance and efficiency.

CLOPS   ←→  Transmission System

Rigetti reported CLOPS for its 40 and 80-qubit systems, shedding light on their quantum processors’ performance. IBM proposed this metric, although specific figures were not provided, suggesting a focus on benchmarking quantum speed. 

Quantum  Volume:  This is a more general measure of both qubit count and the complexity of operations that a QPU can handle. Quantum Volume serves as an aggregate metric that captures both the computational power and reliability of a quantum computer.

Analogous to: the overall performance specifications of a car, which include not just horsepower but also elements like handling, fuel efficiency, and reliability. Quantum Volume takes into account not just the number of qubits but also the complexity of operations the QPU can handle, offering a more holistic view of the quantum computer's capabilities. It's an aggregate metric that assesses both computational power and reliability, analogous to assessing a car's performance across various parameters beyond just raw power.

Quantum Volume   ←→  Overall Performance Specifications

IBM has achieved a Quantum Volume of 256, indicating a significant stride in improving quantum error rates and capabilities.

Quality of Individual Qubits: The performance of a quantum computer is not just about the number  of qubits but also their quality. Factors such as error rates, coherence times, and fidelity are crucial. High-quality qubits are essential in achieving superposition and entanglement, which enable faster and more complex calculations. Their performance directly impacts the processing power and reliability, making low error rates crucial.

Analogous to: The quality of materials, such as the tyres, employed in a car’s construction. Superior materials yield a more durable and efficient vehicle.

Quality of Individual Qubits   ←→  Quality of Material

Microsoft, Google, IBM, and Amazon are working on error-corrected qubits or qubits with lower sensitivity to noise, aiming for robust quantum computation. Xanadu’s emphasis on photonic qubits, Rigetti’s endeavor for high-quality qubits with lower error rates, Intel’s silicon-based qubits, and D-Wave’s metal loops of niobium approach showcase a variety of strategies to enhance qubit quality

Future Challenges in Quantum Computing

Quantum computing faces several critical challenges, including error correction and scalability. Developing effective error correction is crucial, as quantum computers are sensitive to environmental noise that can disrupt computations. Scaling quantum computers to match classical ones, with hundreds or thousands of qubits while maintaining coherence and minimizing error rates, remains a significant task. The production of high-quality quantum hardware, especially qubits and control electronics, is another complex challenge.

Alongside these technical issues, the complexity of quantum algorithms requires innovative computational approaches. Qubit decoherence, due to environmental disturbances, leads to the loss of quantum properties, adding to the difficulties. Addressing these challenges are various initiatives: IBM Research is contributing to quantum computing advancements and standards like CRYSTALS- Kyber and CRYSTALS-Dilithium. Google’s research focuses on developing algorithms for quantum applications, while Microsoft targets post-quantum cryptography. Collaborative projects involving CalTech, the Flatiron Institute, and IBM are exploring the use of AI and ML in solving quantum computing problems.

Quantum-Induced Vulnerabilities of Cryptography and Blockchain

Crypto’s two biggest blockchains use various cryptographic algorithms to secure their respective networks and manage public keys. 

Bitcoin:

• Public-Key Cryptography: ECDSA (Elliptic Curve Digital Signature Algorithm)
• Hash Function: SHA-256 (Secure Hash Algorithm 256-bit)

Ethereum:

• Public-Key Cryptography: ECDSA or Keccak-256
• PoW Mining Algorithm: Casper while the new PoS consensus is based on ”Casper the Friendly Finality Gadget” (FFG)

Advancements in quantum computing pose significant threats to the cryptographic foundations of blockchain networks. Quantum algorithms, such as Shor’s and Grover’s, could potentially break cryptographic algorithms that secure blockchain networks like RSA and ECDSA. 

Shor’s Algorithm:

• Functionality: Finds the private key corresponding to a public key.
• Impact: Direct threat to ECDSA, risking exposure of user wallet private keys.

Grover’s Algorithm:

• Functionality: Searches unsorted databases and solves black-box computational problems.
• Impact: Can potentially halve the bit strength of symmetric cryptography such as SHA-256, requiring a future-proofing upgrade to these algorithms.

The implementation of Shor’s algorithm on a sufficiently large quantum computer can effectively compromise RSA and ECC cryptographic systems, making traditional digital signatures and key exchanges susceptible.

Quantum computers, using Shor’s algorithm, can potentially break asymmetric encryption like RSA and ECC, exposing digital assets on blockchains. Grover’s algorithm enables quantum computers to search for private keys in symmetric encryption, raising the risk of transaction alteration and double-spending.

Quick Explanation of Quantum Hashrate

Bitcoin miners essentially perform a brute-force search for a nonce that, when hashed with the transaction data and the previous block’s hash, produces a new hash below a certain target value. Given that SHA-256 is used, there are 2²⁵⁶ possible hash outputs, which can be considered as the solution space N in Grover’s algorithm. On average, a classical computer needs to check N/2 nonces to find a solution, so for SHA-256, this is 2²⁵⁵ operations.
 

Quantum Mining with Grover’s Algorithm:

Grover’s algorithm would be able to find a valid nonce in roughly N operations, or in the context of Bitcoin mining, 2¹²⁸ operations on a quantum computer to find a valid hash.

Hashrate Calculation:

To calculate a theoretical quantum hashrate, we need to consider how quickly a quantum computer could perform these 2¹²⁸ operations. Presently, even the most advanced quantum computers operate in the timeframe of microseconds (10⁻⁶ seconds) per quantum gate operation (considering error correction and other practical aspects).

If we assume a quantum computer could maintain a stable operation at this speed (a generous assumption given the current technology), then:

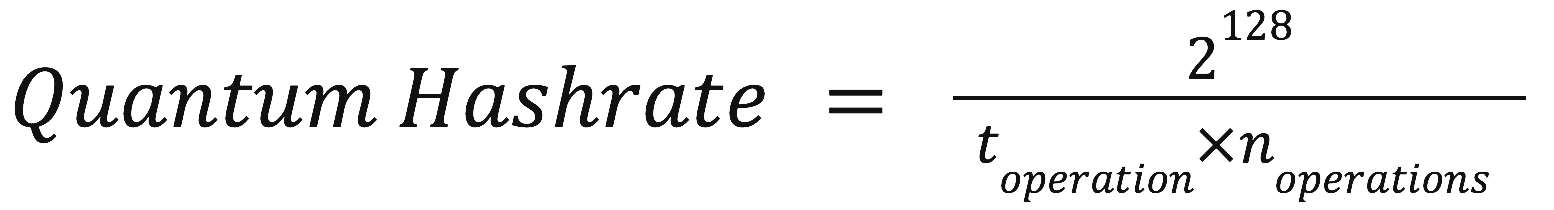
Where:

• t_operation is the time per quantum operation (for example, 10⁻⁶ seconds).

• n_operations is the number of operations needed to find the nonce (2¹²⁸).

Considerations and caveats:

• Error Rate: Quantum computers currently experience significant error rates, which might require repeated calculations to validate results.

• Qubit Stability: Maintaining qubit coherence for the duration of the calculations is a substantial technical challenge.

• Quantum Volume: A quantum computer with a high enough quantum volume (considering qubit count, connectivity, and error rates) to perform these calculations without error is not yet available.

• Scalability: Developing and maintaining a quantum computer of the required scale (number of qubits and error correction capabilities) is a significant challenge.

• Cooling and Energy Consumption: Quantum computers require extremely low temperatures to operate, which can be energy-intensive and technically challenging to maintain.

• Decoherence and Error Correction: Quantum error correction codes and algorithms are required to manage issues with qubit decoherence and errors during calculations.
 

Maintaining Bitcoin Blocktimes

Difficulty adjustment is one of the points to consider when it comes to the impact Grover’s algorithm would have on Bitcoin mining. Bitcoin's difficulty adjustment algorithm plays an important role in maintaining the average block time at approximately 10 minutes. Grover's algorithm, famous for its potential to execute quadratic speedup for unstructured search problems, could theoretically enhance the efficiency of mining by accelerating finding the correct nonce in proof-of-work. If quantum computers accelerate the mining process, the network will automatically adjust the difficulty to compensate for the increased hash power, aiming to preserve the 10-minute block time. However, the effectiveness of this mechanism in a quantum-dominant landscape would depend on how widespread quantum computing becomes among miners. 

The network may require updates or modifications to its difficulty adjustment algorithm to more dynamically respond to the quantum-enhanced hash power, making sure that block times remain stable despite potentially fluctuations in mining speeds.

Implications and Strategic Measures:

• Security Policy: Transition to quantum-resistant algorithms and strategies like larger key sizes or lattice-based cryptography.
• Smart Contracts: Protect Ethereum smart contracts against quantum threats using validation mechanisms like zk-STARKs which rely on Hash functions rather than the hardness of mathematical problems, or other quantum-resistant primitive

Quantum computing can also disrupt blockchain consensus mechanisms. In PoW systems like Bitcoin, quantum computers could solve cryptographic puzzles faster, risking a 51% attack. To counter these threats, the adoption of quantum-resistant hashing algorithms and transitioning to proof-of-stake protocols are crucial. We can summarize these quantum-induced vulnerabilities as follows.

Bitcoin:

• Vulnerable addresses (previously used in a transaction) could have their private keys derived from their public keys using Shor’s Algorithm.
• Mining difficulty could be undermined by utilizing Grover’s Algorithm to manipulate the Proof of Work (PoW) process.

Ethereum:

• Smart contracts and associated DApps, which currently utilize ECDSA or Keccak-256 for establishing trust and verification, risk becoming exposed.
• Ethereum 2.0’s PoS (Proof of Stake) doesn’t escape this risk, as its validation using BLS signatures can be targeted by Shor’s.

In blockchain, PoW requires solving cryptographic puzzles that demand significant computational power in classical contexts. With quantum parallelism, quantum computers can potentially optimize PoW tasks.

Proposals involving coarse-grained boson-sampling (CGBS) for PoW introduce changes to the consensus mechanism: users execute boson-sampling with block-related input states, and these samples are then used for both consensus validation and miner rewarding.

Towards Quantum-Resistant Cryptography

We’ve seen that quantum computers threaten Bitcoin and Ethereum due to their ability to break current cryptographic methods. Shor’s algorithm cracks ECDSA by solving the discrete logarithm problem, exposing private keys from public ones in both Bitcoin and Ethereum. Grover’s algorithm can search databases faster than classical computers, weakening symmetric cryptography like SHA-256 by effectively halving its bit strength.

Future-proofing cryptocurrencies against quantum attacks involves adopting new cryptographic strategies like lattice-based and hash-based cryptography. However, upgrades like these can be complex, requiring widespread network agreement to avoid splits, managing old transactions securely, and ensuring new algorithms work smoothly with existing blockchain functions. Further- more, practical challenges such as maintaining qubit stability, managing errors in quantum calculations, and developing scalable quantum computers remain significant hurdles.

Lattice-Based Cryptography:

• Technical Core: Problems related to finding the shortest vector in a lattice (SVP) – computationally hard problems even for quantum computers.
• Utility: Public key encryptions, digital signatures, and fully homomorphic encryption.

Hash-Based Cryptography:

• Technical Core: Utilizes hash functions (like SHA-256) but in a manner that remains secure despite quantum computational capabilities.
• Utility: Primarily digital signatures.

Code-Based Cryptography:

• Technical Core: Utilizes error-correcting codes as the hard mathematical problem.
• Utility: Post-quantum public-key encryption and digital signatures, though key sizes can be large.

Lattice-Based Cryptography: A Quantum-Resistant Frontier

Lattice-based cryptography, a post-quantum cryptographic approach, operates on grid-based mathematical problems. Core challenges, such as the Learning With Errors (LWE) problem and its related variants, form its foundation, offering resistance against quantum adversarial models. Fault sensitivity analysis (FSA) in lattice-based cryptographic implementations is crucial to assess and mitigate fault-induced information leakages, which are essential for defending against quantum side-channel attacks.

Lattice-based cryptography is gaining attention as a secure method against quantum computing attacks. This type of cryptography, using complex lattice geometries, offers a viable alternative to traditional public-key methods like RSA or elliptic-curve cryptography, which quantum computers could compromise. Its quantum resistance comes from:

• Hard Lattice Problems: The security of lattice-based cryptography relies on the difficulty of solving lattice problems, such as the shortest vector problem (SVP) and the closest vector problem (CVP), for both classical and quantum computers.

• LWE Problem: The learning with errors (LWE) problem, a key part of lattice cryptography, is also believed to be quantum-resistant.

• Algebraic Structure: The algebraic nature of lattices enables the creation of efficient and secure cryptographic algorithms against quantum attacks.

Ethereum’s Hard Fork Proposal for Recovery in a Quantum Emergency

Vitalik recently proposed a potential EIP that could help recover user funds in a scenario where bad actors exploit wallets via quantum computers. In summary the challenge appears that an Ethereum address is defined as keccak(priv_to_pub(k))[12:], where k is the private key, and priv_to_pub is an elliptic curve multiplication to convert the privkey into a pubkey. 

With quantum computers, elliptic curve multiplications become invertible and a public key would ultimately reveal its associated private key. Vitalik’s solution, verbatim, would be to undergo the following process:

1. Revert all blocks after the first block where it’s clear that large-scale theft is happening
2. Traditional EOA-based transactions are disabled
3. A new transaction type is added to allow transactions from smart contract wallets (eg. part of RIP-7560 31), if this is not available already
4. A new transaction type or opcode is added by which you can provide a STARK proof which proves knowledge of (i) a private preimage x, (ii) a hash function ID 1 <= i < k from a list of k approved hash functions, and (iii) a public address A, such that keccak(priv_to_pub(hashes[i](x)))[12:] = A. The STARK also accepts as a public input the hash of a new piece of validation code for that account. If the proof passes, your account’s code is switched over to the new validation code, and you will be able to use it as a smart contract wallet from that point forward.

Quantum Zero Knowledge Proofs (QZK-Proofs)

Quantum Zero-Knowledge Proofs (QZK-Proofs) are an extension of classical Zero-Knowledge Proofs (ZK-Proofs) into quantum computing. They involve two parties: a Prover, who is trying to prove something, and a Verifier, who is trying to validate the claim.

The technical implementation of QZK-Proofs relies on the principles of quantum mechanics, specifically quantum entanglement and quantum superposition. Quantum entanglement allows for a pair or group of qubits to be generated in such a way that the state of one qubit is directly related to the state of the other qubit(s), no matter the distance between them. This is used in QZK-Proofs to create a correlation between the Prover and the Verifier, which allows the Verifier to check the validity of the proof without gaining any additional information.

Quantum superposition allows qubits to exist in multiple states simultaneously. This is used in QZK-Proofs to create a multitude of potential proofs, where only the correct one will be validated when the superposition collapses upon measurement. This improvement enables quantum resistance, improving cryptographic security for the potential future of quantum computers. 

The interaction process between the Prover and the Verifier involves multiple rounds of communication. During these interactions, the Prover constructs a proof that supports the truthfulness of the Prover’s statement. The key property of QZK-Proofs is that the Verifier learns nothing except the validity of the statement being proved similar to original ZK-Proofs. This means that there exists a polynomial-time simulator whose output is indistinguishable from the output of the verifier after communicating with the Prover.

A study by Hirotada Kobayashi from the National Institute of Informatics in Japan gives a clear insight to QZK-Proofs where it has further explored the general properties of quantum zero-knowledge proof systems. The study proves several properties of quantum computational zero-knowledge proofs, such as the equivalence of honest-verifier quantum zero-knowledge and general quantum zero-knowledge. The results of this study are unconditional, where they don’t rely on any computational assumptions.

It’s also important to note that while QZK-Proofs are theoretically possible, their practical implementation is still a subject of ongoing research. As quantum computing continues to evolve, the development and application of QZK-Proofs will undoubtedly play an important role in cryptographic protocols and blockchain technologies.

The transition to QZK-Proofs is not just an improvement but a necessity because of the safety challenges quantum computers create for cryptographic systems. Quantum Zero-Knowledge Proofs are a strategic advancement designed to protect against quantum computing threats, making them a necessary innovation for future-proofing cryptographic security. Their development and implementation are important for maintaining privacy and integrity in a wide range of digital applications if quantum computing becomes a reality (not just in labs).

Quantum-Induced Enhancements of Blockchain 

While much of the discourse in this report has focused on the threats that quantum computing poses to current cryptographic methods, there's an equally compelling narrative about the potential synergies between these two cutting-edge technologies. Far beyond merely making blockchain quantum-resistant, quantum computing holds the promise of revolutionizing blockchain technology in several key areas: performance, scalability, and decentralization.

Performance Enhancement

Quantum computing could dramatically enhance the performance of blockchain networks. Current blockchain systems, particularly those utilizing Proof of Work (PoW) consensus mechanisms, are criticized for their high energy consumption and relatively slow transaction processing times. Quantum computers, with their ability to perform complex calculations at speeds unattainable by classical computers, could optimize the mining process in PoW or even lead to the development of new, more efficient consensus algorithms. 

Scalability Solutions

One of the most pressing challenges facing blockchain technology is scalability. As the number of transactions and users on a blockchain increases, the network can become congested, leading to slower transaction times and higher fees. Quantum computing could offer novel solutions to these scalability issues through more efficient data processing and verification methods (although latency and bandwidth could become a bottleneck). Quantum algorithms are particularly well-suited to parallel processing, which could deliver order of magnitude performance enhancements over existing parallel processing blockchains.

Decentralization and Security

Quantum computing could further enhance the decentralization and security of blockchain networks as the development of quantum-resistant cryptographic algorithms would protect blockchains from quantum attacks, thereby maintaining the integrity and security of decentralized networks. Furthermore, quantum technologies such as Quantum Key Distribution (QKD) could introduce new levels of security in blockchain networks. QKD uses the principles of quantum mechanics to secure communication channels, making it theoretically impossible for an attacker to intercept or decipher the key without detection. Implementing QKD in blockchain networks could ensure not only the secure transmission of data but also enhance the overall trust in blockchain systems.

The degree of decentralization in a quantum-induced Bitcoin network will heavily depend on the accessibility of quantum computing technology. If quantum mining rigs are expensive and scarce (most likely), mining could become centralized among a few wealthy entities or organizations, undermining Bitcoin’s decentralization. To preserve decentralization, the community might encourage the development and distribution of more affordable quantum computing resources or quantum resistant mining algorithms that level the playing field (although this is a challenging and possibly infeasible scenario). 

Quantum Algorithms for Smart Contracts

The application of quantum computing could extend into the realm of smart contracts, making them more efficient and capable of performing more complex operations. Quantum algorithms could enable the execution of smart contracts that are not only faster but also capable of handling more sophisticated logic and calculations.

Conclusion

The intersection of quantum computing and cryptographic technologies heralds a transformative era in information security and digital transactions. As outlined in this report, quantum computing's exponential growth in computational power, demonstrated by advancements in qubit development and quantum algorithms, poses significant challenges to the cryptographic underpinnings of blockchain technologies. The advent of quantum processors, like IBM's Condor and Heron, and the breakthrough improvements in algorithms such as Shor's prime factorization, underscore the urgency in addressing these vulnerabilities.

While quantum computing presents formidable challenges to current cryptographic practices, it also catalyzes the advancement of more secure, quantum-resistant technologies. As quantum computing technology matures and becomes more accessible, we can anticipate its integration into blockchain networks, offering solutions to current limitations while unlocking new capabilities. The collective efforts of researchers, developers, and policymakers will be instrumental in transitioning to a secure digital infrastructure capable of withstanding the quantum computing era. 

References

• General Properties of Quantum Zero-Knowledge Proofs: https://www.nii.ac.jp/qis/first-quantum-era/abstracts/kobayashi.pdf
• Zero-knowledge proof-based device-independent quantum random number beacon: https://phys.org/news/2023-11-zero-knowledge-proof-based-device-independent-quantum.html
• Recent Advances in Zero-Knowledge Proofs in the Quantum Setting: https://simons.berkeley.edu/talks/recent-advances-zero-knowledge-proofs-quantum-setting
• Cloud-Based E-learning: Concepts, and its Beneficial Role During the COVID-19 Dilemma: https://link.springer.com/chapter/10.1007/978-981-19-1610-676
• Shor’s Algorithm – Breaking RSA Encryption: https://blogs.ams.org/mathgradblog/2014/04/30/shors-algorithm-breaking-rsa-encryption/
• Google claims to have reached quantum supremacy: https://www.sciencenews.org/article/google-quantum-supremacy-claim-controversy-top-science-stories-2019-yir
• IBM releases first-ever 1,000-qubit quantum chip: https://www.nature.com/articles/d41586-023-03854-1
• Thirty Years Later, a Speed Boost for Quantum Factoring: https://www.quantamagazine.org/thirty-years-later-a-speed-boost-for-quantum-factoring-20231017/
• IBM Quantum Heron System Two: https://www.techrepublic.com/article/ibm-quantum-heron-system-two
• NIST Announces First Four Quantum-Resistant Cryptographic Algorithms: https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms
• Quantum Computing Challenges: https://thequantuminsider.com/2023/03/24/quantum-computing-challenges/
• Quantum-resistance in blockchain networks Nature Article: https://www.nature.com/articles/s41598-023-32701-6
• Can an SHA-256 Hash be Used as an ECDSA Private Key: https://crypto.stackexchange.com/questions/80926/can-an-sha-256-hash-be-used-as-an-ecdsa-private-key
• Is Ethereum Secure Against an Attack by Quantum Computers: https://ethereum.stackexchange.com/questions/1046/is-ethereum-secure-against-an-attack-by-quantum-computers
• Shor’s Factorization Algorithm - GeeksforGeek: https://www.geeksforgeeks.org/shors-factorization-algorithm/
• Grover’s Algorithm - Wikipedia: https://en.wikipedia.org/wiki/Grover%27s_algorithm
• Quantum Advantage on Proof of Work Arxiv Paper: https://arxiv.org/abs/2105.01821
• Springer Reference: https://link.springer.com/referenceworkentry/10.1007%2F978-1-4419-5906-5_92
• Fundamental Quantum Algorithms: https://github.com/tungabayrak/Quantum-Algoritms-DJ-and-Grover
• Hash-Based Cryptography - Wikipedia: https://en.wikipedia.org/wiki/Hash-based_cryptography
• Quantum Computing Challenges: https://thequantuminsider.com/2023/03/24/quantum-computing-challenges/
• Can an SHA-256 Hash be Used as an ECDSA Private Key: https://crypto.stackexchange.com/questions/80926/can-an-sha-256-hash-be-used-as-an-ecdsa-private-key
• Is Ethereum Secure Against an Attack by Quantum Computers: https://ethereum.stackexchange.com/questions/1046/is-ethereum-secure-against-an-attack-by-quantum-computers
• Shor’s Factorization Algorithm - GeeksforGeek: https://www.geeksforgeeks.org/shors-factorization-algorithm/
  
   

1. Shor, P.W. (1994). "Algorithms for quantum computation: Discrete logarithms and factoring". Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE Comput. Soc. Press. pp. 124–134. doi:10.1109/sfcs.1994.365700. ISBN 0818665807. S2CID 15291489
2. https://blogs.ams.org/mathgradblog/2014/04/30/shors-algorithm-breaking-rsa-encryption/
3. www.sciencenews.org/article/google-quantum-supremacy-claim-controversy-top-science-stories-2019-yir
4. https://www.quantamagazine.org/thirty-years-later-a-speed-boost-for-quantum-factoring-20231017/
5. https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms
6. https://link.springer.com/chapter/10.1007/978-3-031-37679-517
7. https://eprint.iacr.org/2021/1358.pdf
8. Kobayashi, H. (n.d.). General Properties of Quantum Zero-Knowledge Proofs. Principles of Informatics Research Division, National Institute of Informatics. 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan
9. https://phys.org/news/2023-11-zero-knowledge-proof-based-device-independent- quantum.html
10.  Kobayashi, H. (n.d.). General Properties of Quantum Zero-Knowledge Proofs. Principles of Informatics Research Division, National Institute of Informatics. 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan
11.  https://simons.berkeley.edu/talks/recent-advances-zero-knowledge-proofs-quantum-setting
12.  https://link.springer.com/chapter/10.1007/978-981-19-1610-676